 Resetment
Resetment
I can be angry all of the time and can't forget it every single day. I wish I can live alone. only by myself. I don't think I can bu...
aku jatuh cinta untuk merangkai kata kata dan aku terlalu takut akan waktu yang menelan segala kata kataku. tapi, aku masih bisa mengenangnya disini bersama angkasa ini, aku menumpahkannya disini.
 SOCS
Final Review
SOCS
Final Review
Chrysanti Anastasya Silaban 2301877464 Kelas : CB01 Lecture : Henry Chong (D4460) dan Ferdinand Ariandy Luwinda( D4522) apa it...
 Ini galau?
Rasa Untukmu itu memang ada
Ini galau?
Rasa Untukmu itu memang ada
matahari pagi menyapa diriku yang terus terpana. wangi tubuhmu tercium, akupun menahan sambil mengulum senyum. waktu tujuh bulan yang l...
 SOCS
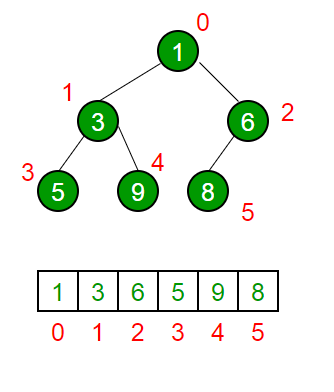
HEAP & TRIES
SOCS
HEAP & TRIES
Hallo semua, kembali lagi dengan materi Data Struct. Kali ini, gue bakalan bahas tentang heap and tries. Q: LAH AGA MUNCUL LU TBTB ...
 SOCS
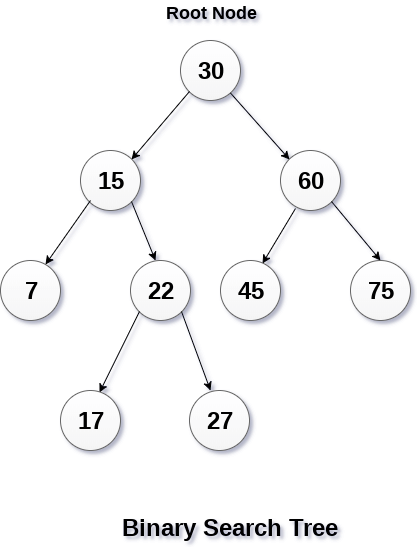
Binary Search Tree(BST)
SOCS
Binary Search Tree(BST)
Binary Search Tree Binary search tree disebut juga kelas pohon biner, di mana node diatur dalam urutan tertentu. nilai semua node di sub-...
 SOCS
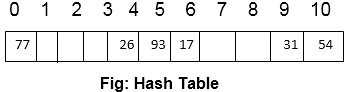
Hash Table & Binary Search Tree
SOCS
Hash Table & Binary Search Tree
Hallo Guys~~ kembali lagi dengan chaca di tugas mata kuliah Data Struct ini. Kali, aku bakalan bahas tentang Hash Table dan Binary Search...
 SOCS
Stack and Queue
SOCS
Stack and Queue
Hallo Semua! kembali lagi nih sama materi data struct yang menyenangkan ini~~ Kali ini bakalan bahas stack sama queue nih! Q :apa sih it...
 SOCS
Linked List
SOCS
Linked List
Hallo Semua! kembali lagi dengan chaca!! Ada yang berbeda dari postingan sebelum-sebelumnya karena postingan kali ini spesial dan sangat...